Patrik Johanssona and A.M.C. Daviesb
aApplied Physics, Chalmers University of Technology, SE-41296 Göteborg, Sweden
bNorwich Near Infrared Consultancy, 75 Intwood Road, Cringleford, Norwich NR4 6AA, UK. E-mail: [email protected]
Introduction
In last year’s August/September issue of Spectroscopy Europe I wrote a column about my “discovery” of computational chemistry and asked if anyone was interested. A satisfying number of readers answered the on-line survey with very positive comments but none more so than Patrik Johansson who e-mailed me about his delight with the column and to assure me that there was “indeed a bunch of scientists out there that do work on IR (and Raman) using both experimental and computational techniques—I am one of them”! This column is the first result of the ensuing e-mail conversation and is due to Patrik. I remain excited by the possibilities of computational chemistry particularly as Patrik thinks that an approach to NIR spectroscopy is indeed possible.
Tony Davies
The topic of that column for those of you whom might have forgotten was “Computational Chemistry” with a pinch of mid-IR—at quite an introductory level. In this column we will now both try to elaborate on this and by a few examples show how and when computational chemistry can be applied to solve fundamental and applied problems together with the right experimental data. With a background in IR spectroscopy and computational chemistry in a chemistry department and today working in a physics environment, which here can be pronounced “Raman”, this is indeed what I do most.
Despite the seemingly rather gruesome restrictions imposed; 0 K temperature, vacuum, only equilibrium etc., computational chemistry methods can surprisingly be applied to real problems at room temperature and for quite complex samples. Having said that and also that many properties are indeed computable by simplifications to the Schrödinger equation, I would like to emphasise that the first thing to consider is in fact to create a representative computer model (or several) of the experimental reality. A typical example is a single benzene molecule to represent liquid benzene. Sometimes it is indeed that simple, but sometimes it is quite more demanding—and now we are talking brain-power, not computational power. As to the latter, often mentioned as an obstacle for everyday use of these methods, we will here try to convince you the opposite. In fact, the calculations in the two first examples shown can today be done on any modern standard desktop PC (or Mac) and the results are obtained within a few days or at most a week (not next year ...). Not bad considering what you actually get. Just to show that the need for supercomputers is not totally alleviated, the last example is a tough example of a non-standard way to create artificial IR and Raman spectra with a little more finesse and accuracy.
Dogmatism and reliance on the numbers might sometimes be heard as a credo of theoretical chemists, but when it comes to computing spectra a pragmatic view is very useful. Of course, any real computational equivalent to a spectroscopy experiment should consider the light–matter interaction in terms of absorbance and scattering, and this way creating really dreadful equations. Luckily another path exists to explore: knowing that the IR spectrum is the consequence of how the dipole moment changes during a specific vibrational mode, we simply (well ...) compute this property instead—for our system at hand. Similarly, the Raman spectrum can be obtained from the changing polarisation with vibrational modes for the system studied. This is indeed the path followed to simple “production” of IR and Raman artificial spectra.
Enough said; let’s show the power in three different examples: 1) conformation equilibrium and distribution of an alkyl chain,2 2) metal ion solvation in non-aqueous solvents3 and last but absolutely not least: 3) the quest for a proper assignment of the CH stretching region—affected by hydrogen bonding or not.4 The latter example also demonstrates how the really classical technique of (partial) deuteration can be used also in our computational approaches—and we top this with including combination and overtones via Fermi resonance. Here is also where we might consider future interaction also with NIR spectroscopists.
Conformation equilibrium
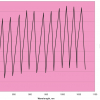
In Figure 1 the Raman spectrum of the room temperature ionic liquid 1-butyl-3-methyl-imidazolium tetra-fluoroborate, [BMI][BF4], is shown and the task of band assignment for the experimental spectrum is seemingly straight-forward; we can by using literature assign the bands arising from the BF4– anion and the different parts, e.g. ring or butyl chain, of the cation [BMI]+, respectively. However, going more into detail we find that there are far too many bands to be assigned—we have ourselves a superposition of different butyl chain conformers. The computational chemist now can be of help—creating a set of models; here nothing more fancy than atomic coordinates for the cation in different conformational states. One way to discriminate the most likely conformers, for any system without using any experiment, is to find those with the lowest energies and then calculate a Boltzmann population. However, the small energy differences and the fundamental restrictions on the calculations make this a less safe path than computing the corresponding spectra. The clever guess of how the conformers should be created, to reduce the number of unique structures needed, is preferably the joint work of the experimentalist and the computational chemist. In Figure 1 we find the artificial spectra resulting from four conformers of [BMI]+. By virtue of using a computational method accurate enough (ca 10 cm–1) we can now assign different bands of the experimental spectrum to different conformations. In addition, the effect of changing a specific dihedral angle in [BMI]+ can be directly related to a spectroscopic signature.
![Figure 1. The Raman spectrum of [BMI][BF4] and computed Raman spectra of [BMI]+ conformers, obtained by altering the two central dihedral angles of the butyl chain to anti (A) or gauche (G) state. (# and * indicate anion bands and possible anion contribution, respectively). Reproduced from reference 2 by kind permission.](/sites/default/files/columns/TD-22_2-F1.jpg)
Remembering that we did not take into account any solvents, everything was done at 0 K and that these results can be obtained in a few days—we hope that also you find this impressive.
A gel electrolyte
Yes, we are now stepping the difficulty level up a bit: we do not even know what species are responsible for the spectrum that we observe—so we must postulate. The particular case shown in Figure 2 is two spectra: one is ethylene carbonate (EC) in propylene carbonate (PC), while the other is added lithium perchlorate (LiClO4) and dissolved in a plastic matrix of poly(methyl methacrylate) (PMMA), together forming a gel. We clearly see that there are two peaks that have shifted neighbours—but what are the origins of these peaks and the reasons for the shifts? The answers to these questions might also reveal important issues at the macroscopic and applied level: what specie is dominant when is comes to carrying around the lithium cation in this system?–a relevant question if we want to use this gel as an electrolyte in a lithium ion battery.

By computing the spectrum of a single EC molecule we can readily assign the peak at ~71 cm–1 to a ring bending mode and the peak at ~894 cm–1 to a ring breathing mode. So much for the EC “reference sample”; now what? One rather well-founded idea is that EC is a solvent that acts with its carbonyl group donating electron density to the metal ion (Li+). Let’s start from there and have a look at such complexes of [Li(EC)x+] with x = 1–6: a probable range of lithium cation coordination numbers in solution. We thus construct at least six computer models (preferably even more to account for different complex geometries for the same x) and compute their spectra. Interestingly we find the x = 4 model with S4 symmetry, Figure 3, to produce relative peak shifts that are extremely similar to those observed experimentally (Table 1). For these large models, up to 60 atoms, we cannot use the most accurate equations to describe the Schrödinger equation, and hence we do not get perfect absolute wavenumbers, but it really does not matter—we would like to know the cause of the observed shifts and now we do! In further support for the [Li(EC)4+] complex the enthalpy of complex formation, quite easily obtained from the calculations, reaches a plateau for x = 4.
| Mode | EC / EC | Gel / [Li(EC) | Relative shift |
| EC ring bending | 717 / 709 | 729 / 721 | +12 / +12 |
| EC ring breathing | 894 / 900 | 904 / 910 | +10 / +10 |
![Figure 3. The obtained [Li(EC)4+] complex with S4 symmetry.](/sites/default/files/columns/TD-22_2-F3.jpg)
Hydrogen bonding: present or not in the CH stretching region
Both the chemistry, but especially the computational methodology is now becoming more complex. So far we have, without mentioning it, considered each vibrational mode to be completely decoupled from all other modes and each movement from the equilibrium atomic distances to be harmonic. We now abandon these simplifications and do account for anharmonicity and (pair-wise) coupling. Why we do this is completely based on a failure—using standard methods we could not reach an unambiguous interpretation of the experimental data. Let us first outline the problem we had at hand: the question is whether or not hydrogen bonding is present in a set of imidazolium-based ionic liquids and, if so, what is the corresponding signature in the CH stretching region (ca 3000 cm–1)? To make a long story short, the breakthrough came when we saw that our calculations, without having any hydrogen bonds present, were able to reproduce the CD region excellently, while the CH region looked rather bad (Figure 4). Thus we were rather certain that there were no hydrogen bonds to complicate the spectra, but at the same time there seemed to be no physical reason for the extra bands in the CH region. The key contribution from the calculations was the notion of large coupling constants between on one hand, the νCH modes and, on the other hand, the R1 and R2 ring modes, their overtones 2R1 and 2R2 and the combination R1 + R2. Thus there might be a presence of overtones and combination bands in Fermi resonance in the CH region and this also explains why the CD and CH regions differ so in their appearance. This finally led to the tentative interpretation of the CH region outlined in Figure 5. How demanding is such a task compared to the previous two presented here? Well, let us just say that each spectrum now is the result of a few thousand calculations instead of only one (even if they are not really comparable). This is absolutely not a trivial task and the use of a supercomputer made this at all possible.


We have deliberately so far not mentioned anything on the choices of ab initio algorithm, basis sets, “Hartree–Fock”, (HF) or “Density Functional Theory” (DFT) etc. First, because we would like you to understand the ideas without getting lost in the complexities, but the real reason is that each problem has its own demand on accuracy and thus any straightforward recommendations are difficult. With this caveat we can tell you (just so you can impress your colleagues!) that all calculations were made using the popular B3LYP hybrid functional (DFT) and medium-sized Pople type basis sets (6–31+G* and 6–311G*)—so nothing fancy or exclusive was ever needed.
As the most common topic of this column is NIR we should make a comment on this as well: the promise of using anharmonic calculations to compute coupling constants and overtones with some accuracy may well be a path worth to stroll—but this lies in the (near) future for us.
References
- A.M.C. Davies, Spectrosc. Europe21(4), 20 (2009).
- R. Holomb, A. Martinelli, I. Albinsson, J.C. Lassègues, P. Johansson and P. Jacobsson, “Ionic liquid structure: the conformational isomerism in 1-butyl-3-methyl-imidazolium tetrafluoroborate ([BMI][BF4])”, J. Raman Spectrosc. 39, 793–805 (2008).https://doi.org/10.1002/jrs.1912
- P. Johansson, M. Edvardsson, J. Adebahr and P. Jacobsson, “Mixed solvent and polymer coordination in PAN and PMMA gel polymer electrolytes studied by ab initio calculations and Raman spectroscopy”, J. Phys. Chem. B 107, 12,622–12,627 (2003).https://doi.org/10.1021/jp035138t
- J.C. Lassègues, J. Grondin, D. Cavagnat and P. Johansson, “New interpretation of the CH stretching vibrations in imidazolium-based ionic liquids”, J. Phys. Chem. A 113, 6419–6421 (2009).https://doi.org/10.1021/jp903160r